はじめに
臨床研究の論文では、その研究に参加した患者/被験者の特徴を示すために「Table 1」として報告するのが一般的です。このTable 1は、論文の読者が他の患者や集団へ結果が適用できるのか(外的妥当性)やバイアスがどの程度あるのか(内的妥当性)を評価するために重要な情報となります。
論文の読者のためにも、著者はTable 1の作法を理解する必要があります。
そこで、本記事ではJournal of Clinical Epidemiologyに掲載された「Table1の作り方」についてのOriginal Article1)を紹介します。
論文を書く際の参考になればと思っています。
Table 1の基本構造
最も単純なTable 1は以下のような構造となっています。
- 列:試験サンプル全体の記述統計量が1列にまとめられている。
- 行:試験の主要な変数が記載されている。
- セル:カテゴリー変数ではn(%)、連続変数では平均値(標準偏差)または中央値(25-75パーセンタイルまたは最小値-最大値)で示されている。
この基本的な構造を研究デザインごとに拡張することで、内的・外的妥当性の評価に必要なより多くの情報を読者に提供することができます。
※ IV: internal validity(内的妥当性)に関する情報、EV: external validity(外的妥当性)に関する情報
次からは基本構造である列、行、セルについて詳細に見ていきましょう。
列
① 列の合計を記述する(EV)
試験サンプル全体の記述統計量を1列にまとめます。列の合計は1番上に記載することが一般的です。
② 曝露で層別化する・・RCT、コホート研究、クロスセクショナル研究(IV)
曝露群と非曝露群を別々の列に表記することで、アウトカムに影響する要因の偏在が直感的にわかります。これにより潜在的な交絡の評価をすることが可能となります。
③ 疾患で層別化する・コントロール群を曝露で層別化する・・ケースコントロール研究(IV)
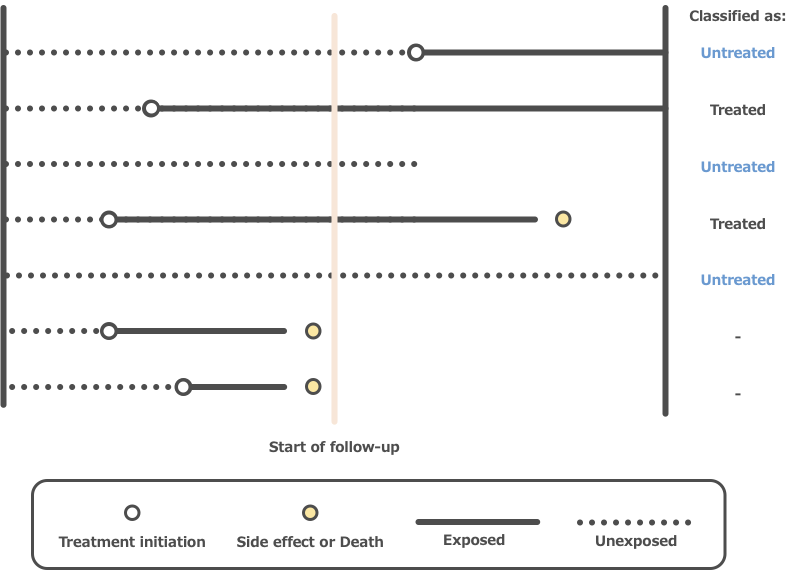
ケースコントロール研究では、ケース群とコントロール群で層別化することで、選択バイアスをある程度評価することが可能です。一方で、ケース群とコントロール群ではアウトカムに影響する要因の分布が異なることが予想されるため、交絡を評価することはできません。ケースコントロール研究における交絡の可能性を評価するためには、コントロール群を曝露によってさらに層別化します。これにより、論文の読者は曝露したコントロール群と曝露していないコントロール群との間での潜在的な交絡因子の分布を比較することができます。(図1、Point2)
④ 統計的推論を含める必要はない
統計的推論として、p値などを記載する列を設けることについては、未だ議論があります。
変数の分布(曝露と非曝露の間など)を統計的に検定することは一般的に行われており、場合によっては投稿先から要求されることもあります。 しかしながら、統計的に有意な差がないことが、変数の分布に差がないことを示すものではありません。有意な差があったとしても、その差が交絡の存在を示すものでもありません。 そのため、交絡因子の評価を目的としてp値を記載することは望ましくありません(図1のPoint3、図2のPoint4)。
行
① 最終解析に含めた全ての変数を表記する(IV)
年齢、性別、併存疾患など解析に使用した変数は全て列挙をする必要があります。
② 「収集時」ではなく「分析時」で変数を要約する(IV)
変数が収集された方法とは異なる方法で分析される場合(例:連続変数をカテゴリー化するなど)、一般的には「分析時」の方法で要約します。しかし、連続変数をカテゴリー化した場合は、連続変数と比較して測定誤差や残余交絡を引き起こす可能性があります。そのため、分析時のカテゴリー変数と測定された元の変数の両方を表示することで、カテゴリー化の決定とそれによって引き起こされるバイアスがより明確になります(図1、Point4;図2、Point6)。
③ その他列に含めることを考慮する項目
- サンプリング変数(IV):サンプリングに使用された変数、研究参加や追跡不能に影響を及ぼす可能性のある変数
- 可能性のある交絡因子(IV)
- 可能性のある効果修飾(EV)
これらの変数を含めることで、最終的な分析に含まれない変数による残余交絡や選択バイアスに関する情報を読者に提供することができます。例えば、ケースコントロール研究では、研究登録時の選択バイアスの存在を示す可能性がある変数(例:病院ベースのケースコントロール研究における自宅から病院までの距離)の行を含めることが有用です(図1、Point6)。
生存時間解析を含む研究では人年の要約(総計、平均、中央値)と打ち切りの理由の要約を書く必要があります。打ち切りの理由が曝露群と非曝露群で異なる場合、打ち切りは内的妥当性を脅かす情報となり得るからです。
また、観察期間が異なれば、曝露/介入の効果も異なる可能性があるので、平均人年は外的妥当性に関する情報となります。
セル
表の読みやすさや列間の比較を容易にするために、セルの内容は視覚的な混乱を減らすことに留意します。
①カテゴリー変数のn(%)を表記する(IV, EV)
カテゴリー変数の場合はパーセントのみを表示し、列のヘッダーにN数を表示します。
② 連続変数は「平均値(SD)」で表す。分布の非対称性がある連続変数は、「中央値(min-max)」や「中央値(25 percentile -75 percentile)」で表示する。(IV, EV) (図1、Point7)
分布に関する詳細な情報は、読者にとって内的妥当性・外的妥当性を評価するのに重要な情報となりす。
- データ収集時に測定誤差が生じて内的妥当性が損なわれていないかどうか。
(例:血圧測定値の分布が予想よりも低い場合) - あるデータが効果推定値に過度の影響を与えていないかどうか
(内的妥当性を損なう可能性がある) - 標本の分布がtarget populationと比較してどのように異なっているか。
(結果の外的妥当性を評価するのに役立つ)
③ 正確さが要求される場合を除き、パーセント表示は小数点以下を四捨五入して表示する。(図1、Point5)
④ 空欄とした理由の明示
情報が収集できていなかったり、値が欠損したりしている場合など、意図的にセルを空白にしたということを示す必要があります。その場合は空白のセルのまま提示するのではなく、陰影や特定の文字(ピリオドやダッシュなど)でセルを埋め、表の脚注にその理由を明示します。
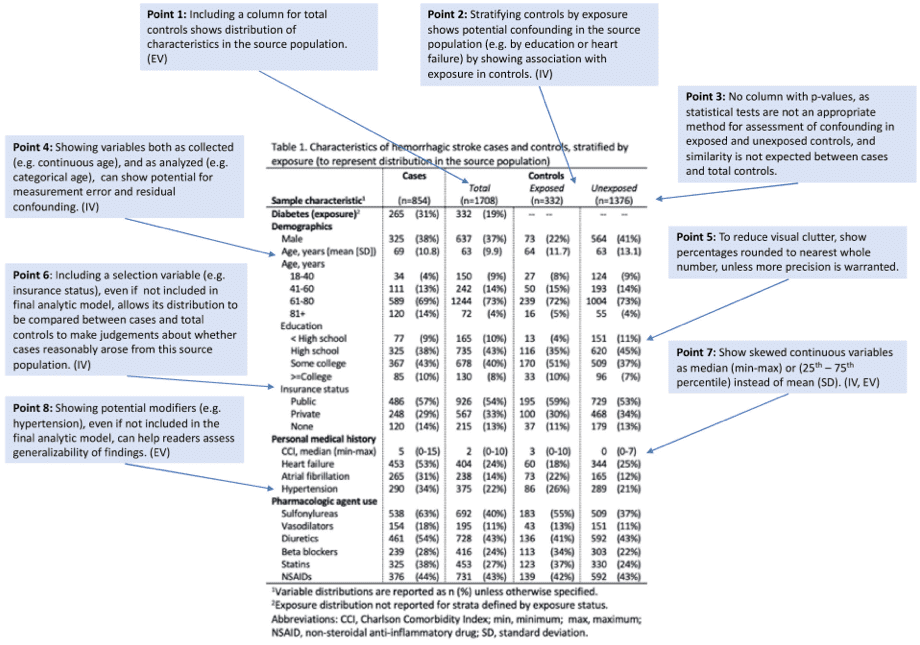
図1. Example construction of Table 1 for a hypothetical case-control study.(引用1)Figure 2より引用)
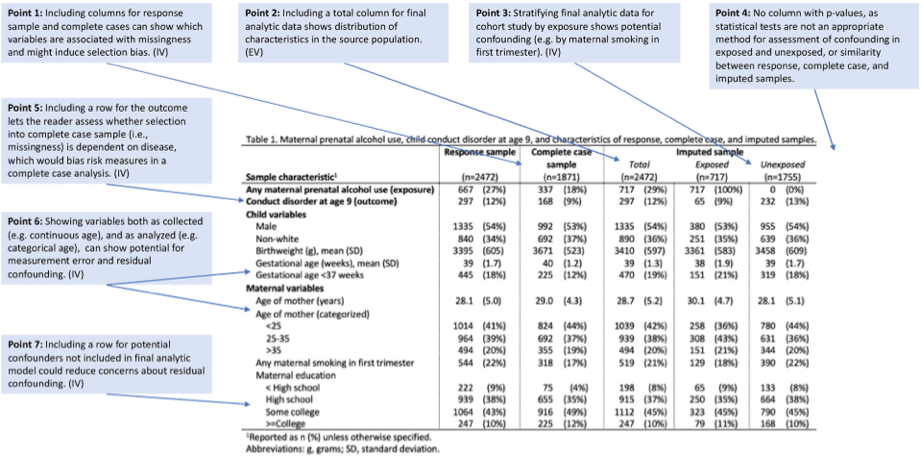
図2. Example construction of Table 1 for a hypothetical cohort study with missing data.(引用1)Figure 3より引用)
解析別の注意点
欠損値がある場合
- 列:Complete cases、partial cases、one imputed datasetを示す(IV)
- 行:アウトカム変数を含める
欠損値が懸念されるのは、欠損値を持つ対象者のデータは除外され、欠損値を持たない対象者のみが分析対象として「選択」されるからです。このことは妥当性に影響を与える可能性があり、選択バイアスとして検討します。
Table 1に欠損値を持つ対象も含めた観測値(partial cases)と欠損値を持たない対象者を除外した観測値(complete cases)を示す列を追加することで、測定された変数が欠損/選択と関連しているかどうかを評価することができます(図2、Point1)。
その上でアウトカム変数の行を追加することで、欠損値の対象を除外した場合にアウトカムの分布が変化するかどうかを判断することができます。
これらの測定された変数のうち、アウトカムが選択と関連しているかどうかを示す行を含めることは特に重要です。
欠損値の取り扱いにはいくつかの分析方法があります(complete case analysisやmultiple imputationなど)。Table 1にpartial casesとcomplete casesを示すことで、著者がどの分析方法を選択するべきなのかを明確にすることもできます。例えば、Table 1でpartial casesとcomplete casesの間に曝露の分布以外の違いがない場合、complete case analysisではバイアスが発生しない可能性が高いです。しかし、欠損/選択がアウトカムに関連している場合、complete case analysisではバイアスが発生してしまうため、不適切となってしまいます。
クラスターデータを使う場合
- 列:クラスターと個別の観測値を分けて示す(EV)
- 行:クラスターごとのn数とサンプリング率を示す(EV)
マルチレベル研究や反復測定法を用いた研究などのクラスター化されたデータを用いた研究では、2つのsource populationが存在します。1つはクラスターレベルで、もう1つは個々の観察レベルです。そのため、それぞれのpopulationについて記述統計を示す必要があります。これにより、各変数について、クラスター自身がtarget populationのクラスターと類似しているかどうかを読者が判断できるため、外的妥当性の評価につながります。
交互作用、効果修飾に関心がある場合
- 列:曝露と修飾因子で層別化する(IV)
- 行:列全体における曝露と修飾因子の分布を示す(EV)
交互作用、効果修飾、または層別化された結果に関心がある場合、Table 1は層に関する詳細な情報を示す必要があります。例えば、性差や人種差の研究では、サンプル全体ではなく性別や人種ごとに追加の層を設けてTable 1を表示します。さらに、曝露変数と層別変数のいずれかで交絡が生じている可能性があるため、曝露変数と層別変数の両方の層に応じて、すべての変数の分布を示すことが望ましいです(例:二値変数の曝露変数と二値変数の層別変数であれば4列追加する)。
最後に
論文の読者が適切に内的・外的妥当性を評価するために、著者はTable 1に必要な情報を示すことが求められます。
これらの情報を書く際は、単に必要事項を列挙するだけでなく、読者の立場に立って読みやすさも意識する必要もあります。
例えば、以下のような点に気をつけるとよいでしょう。
- 列の数が少なく、セルの内容が単純になるよう気を付ける(小数部を最小限にするなど)
- 列や行間の比較を容易にするために、行-列間の罫線を引くことを避ける。
- 列や行間の境界をわかりやすくするために陰影を使用する。
- 小数部の位置に沿ってデータを整列させる。(「1.5と1」ではなく「1.5と1.0」など)
本記事と紹介した論文1)がTable 1を作成する際の参考になればと思っています。
※データックでは論文執筆に関するご相談も受け付けていますので、お気軽にお問い合わせください。
引用
- Hayes-Larson E, Kezios KL, Mooney SJ, Lovasi G. Who is in this study, anyway? Guidelines for a useful Table 1. J Clin Epidemiol. 2019;114:125-132.
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6773463/